Cập nhập ngày : 21/07/2025 bởi
Khối nón là hình học quen thuộc trong toán học và một trong những kiến thức trọng tâm của nhiều bạn học sinh cần phải nắm rõ những vấn đề liên quan đến khối nón. Tuy nhiên vẫn nhiều người chưa nắm rõ công thức tính thể tích khối nón một cách chính xác và đầy đủ nhất. Bài viết dưới đây sẽ giúp bạn tổng hợp các công thức tính thể tích khối nón tròn xoay, khối nón cụt, khối nón có đường sinh,… mà bạn có thể tham khảo.
Hình khối nón là một hình học không gian được tạo thành từ một mặt đáy là hình tròn và một mặt bên là mặt cong, thu hẹp dần đến một điểm gọi là đỉnh. Hình khối nón được hình thành khi quay một tam giác vuông quanh một cạnh góc vuông cố định (trục quay).
Trong thực tế, hình nón xuất hiện nhiều trong cuộc sống như: nón lá, nón sinh nhật, biểu tượng tổ chức, hình dáng trang sức, kiến trúc,...
Các loại hình khối nón phổ biến
Hình nón tròn xoay:
Là hình nón được tạo ra khi quay một tam giác vuông quanh một cạnh góc vuông. Trục quay đi qua đỉnh và tâm của đáy, tạo ra một hình nón có mặt đáy là hình tròn và đỉnh nằm trên trục vuông góc.
Hình nón cụt:
Là phần còn lại khi cắt một hình nón tròn xoay bằng một mặt phẳng song song với đáy và loại bỏ phần đỉnh. Hình nón cụt có hai đáy tròn song song và một mặt bên cong.
Hình nón xiên:
Là hình nón có đỉnh không nằm trên trục vuông góc với đáy. Đỉnh được nối từ một điểm bất kỳ ngoài tâm của hình tròn đáy, tạo ra một hình không đối xứng.
Dưới đây sẽ là công thức tính thể tích khối nón chi tiết theo từng loại:
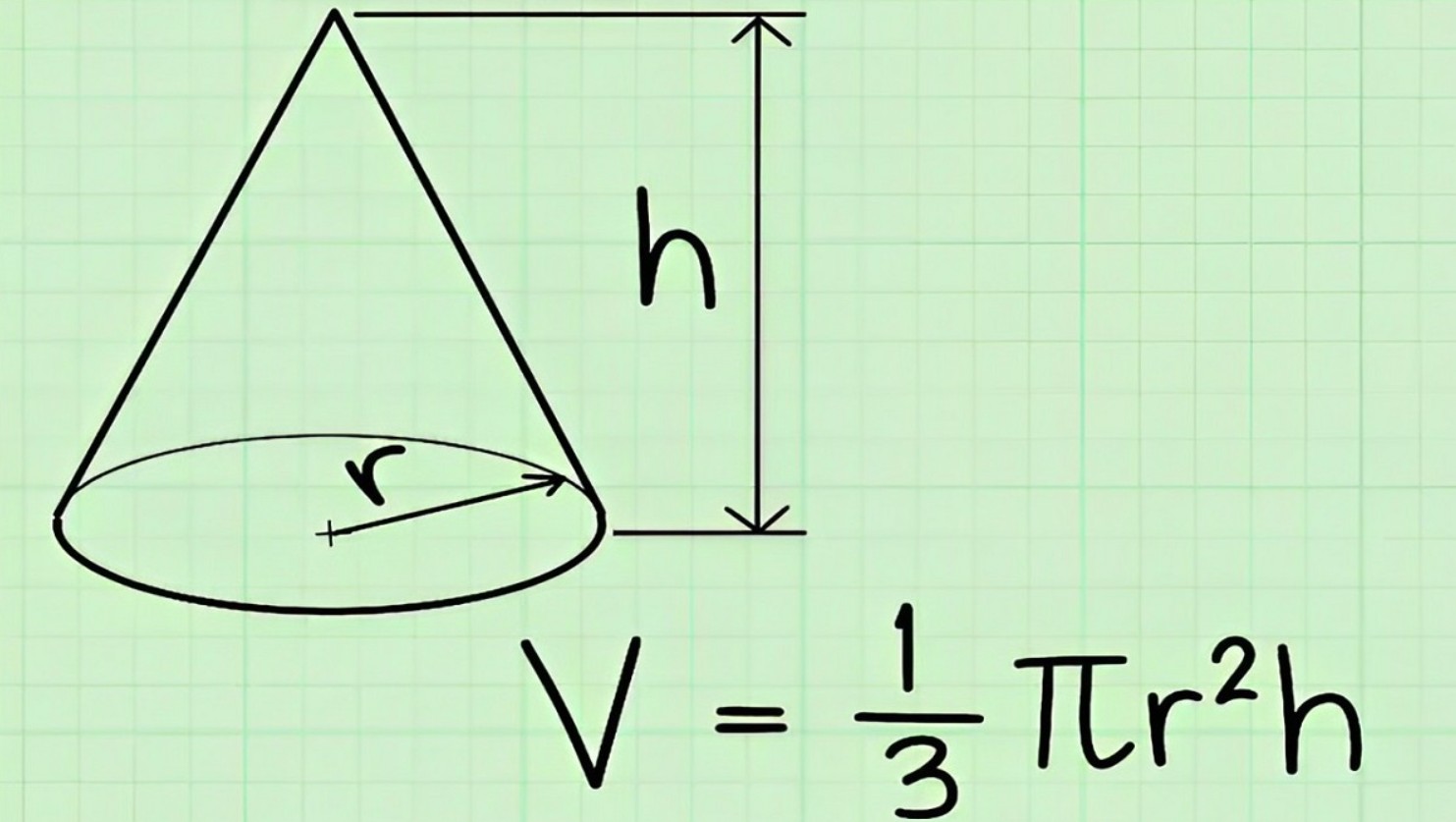
Ví dụ công thức thể tích khối nón thường
Công thức:
\( V = \frac{1}{3} \pi r^2 h \)
Trong đó:
VVV: thể tích khối nón
rrr: bán kính đáy
hhh: chiều cao (vuông góc từ đỉnh đến đáy)
π\piπ: hằng số Pi ≈ 3.14
Ví dụ:
Cho một hình nón có bán kính đáy r=4cmr = 4cmr=4cm, chiều cao h=5cmh = 5cmh=5cm, khi đó:
$$ V = \frac{1}{3} \pi \times 4^2 \times 5 = \frac{1}{3} \pi \times 16 \times 5 = \frac{80}{3} \pi \approx 83.78 \, \text{cm}^3 $$
Khối nón cụt là phần còn lại sau khi cắt một hình nón bởi một mặt phẳng song song với đáy.
Công thức:
\( V = \frac{1}{3} \pi h (R^2 + r^2 + Rr) \)
Trong đó:
RRR: bán kính đáy lớn
rrr: bán kính đáy nhỏ
hhh: chiều cao giữa hai đáy
π\piπ: số pi ≈ 3.14
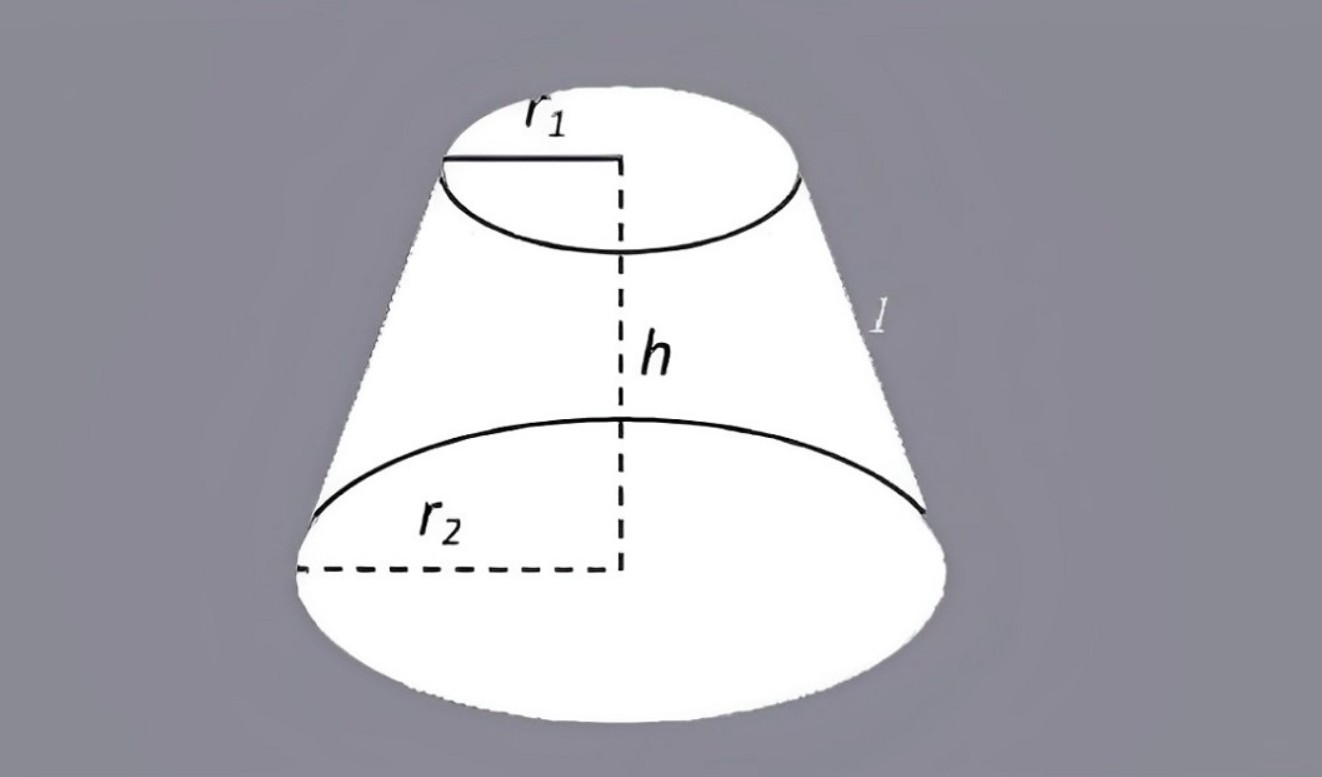
Bài ví dụ về thể tích khối nón cụt
Một khối cầu ngoại tiếp hình nón là hình cầu bao trọn toàn bộ hình nón, tức là cả đỉnh và đáy của hình nón đều nằm trên mặt cầu. Trường hợp này thường áp dụng cho hình nón tròn xoay (nón đều).
Giả sử hình nón có:
r: bán kính đáy
h: chiều cao
Ta tính đường kính khối cầu ngoại tiếp bằng độ dài đường sinh từ đỉnh đến tâm đáy:
l = √(r² + h²)
Bán kính của khối cầu ngoại tiếp là:
R = l / 2 = √(r² + h²) / 2
Áp dụng công thức thể tích khối cầu:
V = (4/3) × π × R³
Thay R vào, ta có công thức thể tích khối cầu ngoại tiếp hình nón:
V = (π / 6) × (r² + h²)3/2
Lưu ý: Công thức này chỉ áp dụng với hình nón tròn xoay (đỉnh nằm trên trục vuông góc với đáy).
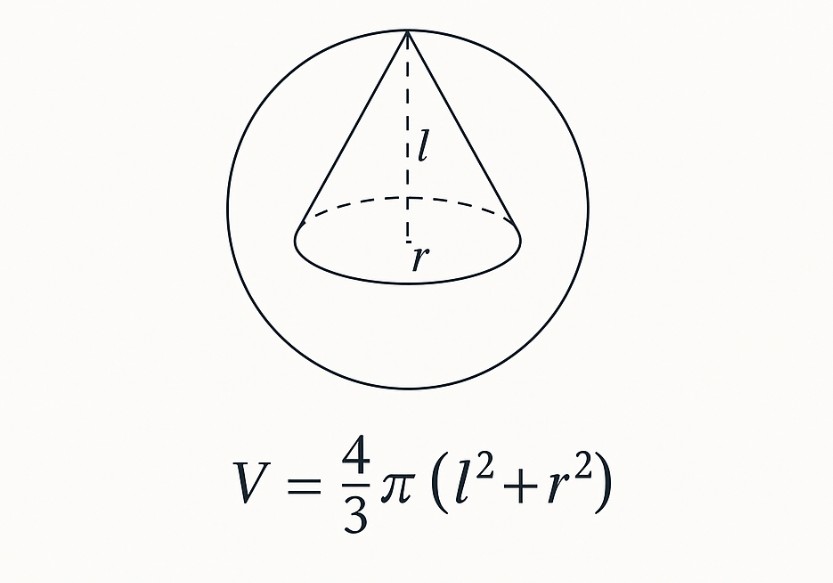
Ví dụ Công thức tính thể tích khối cầu ngoại tiếp hình nón
Trước khi thực hiện tính thể tích khối nón, bạn cần xác định rõ hình dạng và các thông số được biết của hình nón đó.
Trường hợp 1: Hình nón có bán kính đáy r và chiều cao h
Đây là hình nón thường gặp nhất. Thể tích được tính bằng công thức:
\( V = \frac{1}{3} \pi r^2 h \)
Trong đó:
r là bán kính đáy của hình nón
h là chiều cao (vuông góc từ đỉnh đến đáy)
Trường hợp 2: Hình nón có bán kính r và đường sinh l
Khi chỉ biết đường sinh và bán kính, bạn cần tính chiều cao h trước bằng định lý Pythagoras:
\( h = \sqrt{l^2 - r^2} \)
Sau đó thay vào công thức ở trường hợp 1:
\( V = \frac{1}{3} \pi r^2 \sqrt{l^2 - r^2} \)
Trường hợp nâng cao: Hình nón có dạng thay đổi bán kính theo chiều cao (nón không đều)
Lúc này cần dùng tích phân để tính thể tích:
\( V = \int \pi [r(h)]^2 \, dh \)
Trong đó r(h) là bán kính tại mỗi độ cao h. Trường hợp này thường gặp trong các bài toán hình học không gian nâng cao hoặc trong kỹ thuật.
Sau khi đã nắm được cách tính thể tích khối nón thì bạn có thể tham khảo thêm một số công thức liên quan để thuận tiện trong việc tính toán và giải bài tập:
Đường sinh của hình nón là một đường cong trong hình nón được sử dụng để tính thể tích hoặc diện tích bề mặt. Trong toán học thì đường sinh của hình nón được nhận diện thông qua hai điểm trên đường sinh và một điểm trên mép của hình nón.
Bán kính đường tròn đáy của hình nón có thể tìm được qua công thức sau:
Đường cao của hình nón được xác định bằng cách nối một đường thẳng giữa trung điểm của đường tròn đáy với điểm trên đỉnh của hình nón.
Bán kính đáy của một hình nón được xác định thông qua cách tính khoảng cách giữa trung điểm của đường tròn đáy và bất kỳ điểm nào trên đường tròn đáy. Bên cạnh đó bạn cũng có thể xác định bằng cách sử dụng công thức diện tích của hình nón và chiều cao của nó.
Để hiểu và ghi nhớ công thức tính thể tích khối nón bạn có thể tham khảo một số bài toán và lời giải chi tiết ngay sau đây:
Lời giải bài toán trên như sau
Đường sinh: Đường sinh của hình nón là đường nối tâm đáy đến trục cao nhất của hình nón. Đường sinh của hình nón có chiều dài là √(4a^2 + 3a^2) = √(25a^2).
Diện tích xung quanh: Diện tích xung quanh hình nón là tổng của diện tích của một vòng tròn và một hình tròn. Diện tích xung quanh của hình nón có công thức là \( A = 2\pi r \ (r = 4a) + \pi r^2 = 2\pi(4a) + \pi(4a^2) = 28\pi a^2 \).
Diện tích toàn phần: Diện tích toàn phần của hình nón là tổng của diện tích của một vòng tròn và một hình trụ. Diện tích toàn phần của hình nón có công thức là \( \pi r^2 + \pi r^2 h = \pi (4a^2) + \pi (4a^2)(3a) = 52\pi a^2 \)
Thể tích: Thể tích của hình nón có công thức là $$ V = \frac{1}{3} \pi r^2 h = \frac{1}{3} \pi (4a^2)(3a) = 4\pi a^3 $$
Lời giải bài toán trên như sau
Để tính diện tích xung quanh của hình nón, trước tiên ta cần xác định được độ dài quanh viền và chiều cao của nón.
Theo giả thiết cho góc giữa đường sinh và mặt phẳng đáy là 30º thì ta có thể áp dụng công thức
h = l * sin(30º)
Tiếp đó sẽ sử dụng diện tích xung quanh của hình nón là tổng của diện tích mặt trên và diện tích quanh viền:
\( A = 2\pi l h + 2\pi \left(\frac{l}{2}\right)^2 = 2\pi l h + \frac{\pi l^2}{2} \)
Trong đó, (l/2)^2 là diện tích mặt trên của hình nón.
Lời giải bài toán trên như sau
Giả sử chiều cao của khối nón ban đầu là h và bán kính của đáy là r. Thì thể tích của khối nón ban đầu được tính theo công thức:
\( V = \pi r^2 h \)
Nếu như tăng bán kính của khối nón lên 2 lần, bán kính mới sẽ là 2r và thể tích mới sẽ là:
\( V' = \pi (2r)^2 h = 4 \pi r^2 h = 4V \)
Với giả thiết thể tích ban đầu bằng 30π nên thể tích mới bằng 4 * 30π = 120π.
Lời giải bài toán trên như sau
Khi quay tam giác ABC xung quanh cạnh AB thì khối nón mới sẽ được tại ra với đường sinh là cạnh AB = 2a.
Chiều cao của khối nón là chiều cao của tam giác ABC từ đỉnh A, có thể tính theo công thức h = √(a^2 – (a/2)^2) = a√(3)/2.
Thể tích của khối nón là tổng của diện tích xung quanh và diện tích mặt trên với công thức chi tiết như sau:
V = π * (2a)^2 * h/3 + π * (2a/2)^2 * h/2
= 2π * a^2 * h/3
= 4π * a^3 / (3√3)
Lời giải bài toán trên như sau
Thể tích của khối nón có thể tính bằng diện tích của một mặt cắt qua trục của nón, chia cho 2.
Diện tích mặt cắt qua trục của nón là diện tích của tam giác vuông cân tại trục của nón. Do đó, diện tích mặt cắt qua trục của nón có công thức là:
S = a^2 * √(3)/2
Từ đó suy ra thể tích của khối nón là:
V = S * 2a / 2 = a^3 * √(3)
Kết luận: đáp số thể tích của khối nón biết thiết diện qua trục của nó là tam giác vuông cân có cạnh huyền bằng 2a là a^3 * √(3).
Lời giải bài toán trên như sau
Thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 là:
V = π * (5/2)^2 * 4 / 3 = 10π
Kết luận đáp số thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 là 10π.
Lời giải bài toán trên như sau
Thể tích của khối nón là 4π, chiều cao của nón là 3, vậy diện tích của đáy của nón là:
S = 4π / 3 = 4π / (1/3 * chiều cao)
Bằng cách sử dụng công thức diện tích hình tròn ta có thể tìm ra bán kính đường tròn đáy của khối nón
S = π * r^2
Thông qua việc so sánh hai công thức nêu trên ta có thể tìm ra bán kính đường tròn đáy của khối nón cụ thể như sau:
π * r^2 = 4π / (1/3 * 3)
r^2 = 4 / (π * (1/3 * 3))
r = √(4 / (π * (1/3 * 3))) = √(4 / (π * 1)) = √(4 / π)
Kết luận đáp số bán kính đường tròn đáy của khối nón là √(4 / π).
Trên đây là thông tin chi tiết về hình nón và các công thức tính khối nón mà chúng tôi đã tổng hợp được. Ta có thể thấy khối nón có rất nhiều loại với cách thể tích khối nón khác nhau nên cần phải thật chú ý khi lựa chọn công thức tính toán. Hy vọng bài viết trên giúp bạn tính toán dễ dàng và nhanh chóng hơn thông qua công thức và ví dụ cụ thể liên quan đến thể tích khối nón
Đểm xem thêm các sản phẩm ưu đãi và nhận ngay mã giảm giả hay truy cập ngay vào đây : Mã giảm giá Shopee
![[2025] Phí Trễ Hạn HD Saison Là Bao Nhiêu? Trễ Bao Lâu Bị Nợ Xấu?](https://chiasevaytien.net/pictures/2025/05/05/1746426597amvdfe.jpg)
![[Sự thật] Hội bùng tiền App Vay Online như thế nào](https://chiasevaytien.net/pictures/2022/03/14/1647194156fknjks.webp)
Bạn hãy là người bình luận đầu tiên !